Q值不高的LC谐振电路，通常是导线电阻是影响Q值的主要因素。把线阻单独表示出来，就是这样的电路：

 

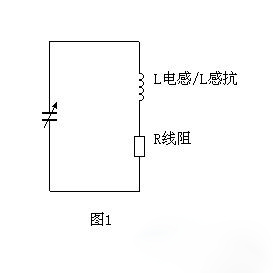
     按这个电路，谐振时Q值的计算是：
 式1：    Q值 = L感抗 / R线阻

    这个电路在应用中，经常被等价为另一个电路：

 
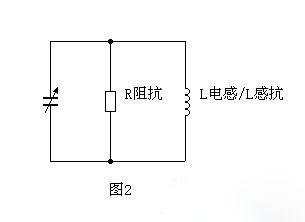
     图2的电路在分析很多问题时很有用。但谐振时Q值的算式变成这样：
 式2：    Q值 = R阻抗 / L感抗

    两种形式都很好理解。图1式1是串联分压模型，电感分压是电阻分压的Q倍。图2式2是并联分流模型，电感分流是电阻分流的Q倍。

    图2和式2对一个现成的电路有很好的描述力，但为设计电感带来很大的迷惑。

    按照图1式1，感抗与越大，Q值越大。而按图2式2，感抗越小，Q值越大。

    到底感抗越大越好还是越小越好？

    原来，图2的R阻抗，是在电感确定之后才确定的，是从Q值反算出来的：
 式3：    R阻抗 = Q值 * L感抗

    例如按图1，R线阻=1欧，L感抗=20欧，则有Q值=20。如果等效成图2电路，就有R阻抗=20欧*Q值=400欧。

    当线阻是影响Q值的主要因素时，加大电感可以提高Q值，因为电感量的增加比线阻的增加更快。在电感量较小时，电感量是与匝数的平方成正比的。

    上例把匝数加大一倍（原来的2倍），那么R线阻=2欧（原来的2倍），L感抗=80欧（原来的4倍），便有Q值=40（原来的2倍）。折算为图2，R阻抗=L感抗*Q值=80欧*40=3200欧（原来的8倍）。

    但是，LC谐振回路要接负载。负载经常都是真家伙并联分流的。不考虑线阻时，和图2一样的结构：

 

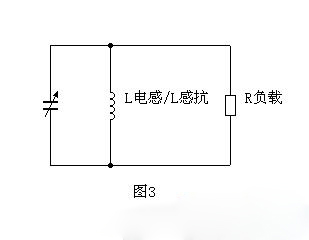
     这时Q值的计算方法又和式2一样结构：
 式4：    Q值 = R负载 / L感抗

    因为R负载是真实的，不是反算出来的，所以式4表明L感抗越小，Q值越高。

    把串联线阻和并联负载都画出来，就是这样：

 

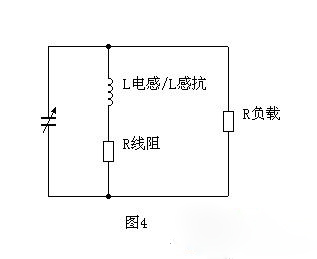
     L电感正好夹在R线阻和R负载之间。为了Q值高，L感抗要尽量比R负载小，以便获得尽量大的分流。同时，L感抗要尽量比R线阻大，以便获得尽量大的分压。

    如果R线阻=1欧，R负载=1万欧，那么L感抗最好就是100欧。这样，能量被R负载分流去1%，被R线阻分压1%，共损失1/50，最后得到Q值=50。

    感抗的最佳值，是R线阻与R负载的几何平均值。

    如果R线阻=1欧，R负载=1万欧，提高感抗到200欧，那么分流消耗为1/50，分压消耗=1/200，合并消耗1/40，于是Q值=40，下降了。

    由此可见，靠拼命提高电感来提高空载Q值是不可取的。式1就是算空载Q值的。如果感抗太高，一接上负载分流，Q值立即崩溃。

    所谓“空载Q值越高，有载Q值就越高”的说法是站不住脚的。用提高电感来提高Q值，必须在合理的范围之内。如果是减小线阻提高Q值，那是无害的，当然对提高有载Q值也有好处。

    R线阻，R负载，L感抗三者的关系，已经规定了电路Q值的上限。要提高有载Q值，主要还是在三者之间谋划。

    这一种关系同时论证了高频下需要用小的电感配合小的电容。感抗是会随着频率升高而升高的。感抗升得太高，超出合理范围，有载Q值会明显下降。

    我们还可以看容抗，谐振时容抗与感抗是相等的。空气可变电容的变化最直观。经常可以发现，当可变电容调得越来越小，就会越来越失去调谐能力。电容太小确实会失去对电路的操控能力，有这里说的原因，也有别的原因。随着电容变小，如果发现空载的选择性越来越好，而有载的选择性越来越差，那就是这里的说原因：感抗太大。

    最后补充：在高Q值的领域，影响Q值的损耗不仅线阻。在各种损耗中，有的可以等价为串在线圈上的电阻，但也有与电压相关的损耗，例如电容漏电，它本来就是一个并在线圈上的电阻。负载中也不仅限于并联方式，也会有串联的因素。什么属于分压消耗，什么属于分流消耗，如何针对性地调整电感量，此类高级课题属于后话。矿石机的实际情况更复杂，除了空载、有载之处，还有天线地线的影响。